思路：

递归构建二叉树，并输出先序排列。

首先要知道后序排列、中序排列是怎么构成的。
后序排列是先左，然后右，最后根；中序排列是先左，然后根，最后右。

依此我们可以确定后序排列中的最后一个一定是这个树的根，我们可以将根的左右两边分为两个子树，左子树和右子树，在中序排列中在根左边的是左子树，在右边的是右子树，最后便可构建出二叉树。

例如样例：
给出了中序排列为 BADC，后序排列为 BDCA，可以看的后序排列的最后一个字母是 A，那么说明 A 是根，然后我们在中序排列中找到 A，此时 A 左边的是左子树里的，右边是右子树里的。

所以现在可以转换为：

• 左子树：中序排列为 B，后序排列是 B。
• 右子树：中序排列为 DC，后序排列是 DC。

接着我们一直递归直到不能递归就能构建出二叉树了。

样例可能有点小不好理解这里给出另一组再进行一次解释。
当中序排列为 CBEAGDF，后序排列为 CEBGFDA 时。
后序排列的最后是 A，所以 A 是根，然后再确定左、右子树。

然后当有左子树时，把它当做一个独立的二叉树处理，查询它的后序排列，确定根，然后接着确定这个二叉树的左、右子树；当有右子树时进行一样的操作。

本树构建过程画出如下的图。

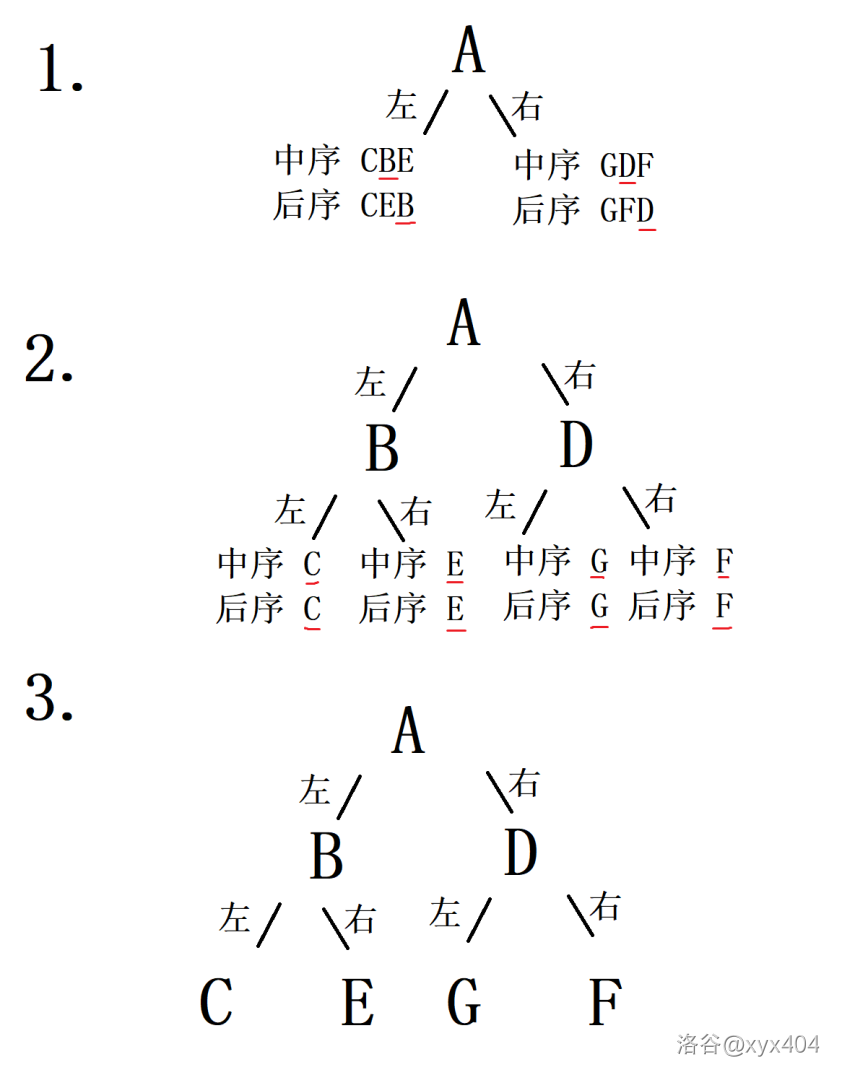
当然在代码中我们无法同时处理左、右两个子树，所以在代码中我们要将它们分别处理。

总的来说就是由后序排列确定根，由中序排列确定左子树和右子树，然后继续递归直到不能递归。

为了输出先序排序，我们可以先把每次的根输出，然后处理左子树，最后再处理右子树，因为先序排序是先根，然后左，最后右。

代码：

#include<bits/stdc++.h>
using namespace std;
#define LL long long
#define itn int
#define ull unsigned long long 
string a,b;
struct node{
	char data;
	int l,r;
}tree[60];
void jiangshu(int al,int ar,int bl,int br,int k){
	int root=a.find(b[br]);
	tree[k].data=b[br];
	cout<<tree[k].data;
	if(root>al){
		tree[k].l=2*k;
		jiangshu(al,root-1,bl,br-ar+root-1,2*k);
	}
	if(root<ar){
		tree[k].r=2*k+1;
        jiangshu(root+1,ar,br+root-al,br-1,2*k+1);
	}
}
int main(){
    cin>>a>>b;
    jiangshu(0,a.size()-1,0,b.size()-1,1);
    return 0;
}