洛谷题解贪心题解:P13457Minimum Scalar Product
xyx404
简要题意:
给定两个 vector,v1=(x1,x2,⋯,xn) 和 v2=(y1,y2,⋯,yn),要求最小化标量积 x1×y1+x2×y2+⋯+xn×yn,两个 vector 中的元素可以任意更改位置。
思路:
将 v1 和 v2 分别按升序和降序进行排序,然后计算即可。
证明在最后。
代码:
#include<bits/stdc++.h>
using namespace std;
#define LL long long
#define itn int
#define ull unsigned long long
int T;
LL a[810],b[810];
int cnt;
int main(){
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>T;
while(T--){
cnt++;
int n;cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++)cin>>b[i];
sort(a+1,a+1+n);
sort(b+1,b+1+n);
LL ans=0;
for(int i=1,j=n;i<=n;i++,j--){
ans+=a[i]*b[j];
}
cout<<"Case #"<<cnt<<": "<<ans<<"\n";
}
return 0;
}
|
证明:
尽管比较显然,但我们还是证明一下,考虑反证法。
假设存在另一种配对方式,使得标量积比 v1 升序,v2 降序的配对方式更小。
设 v1 按升序排序 x1≤x2≤⋯≤xn,v2 降序排序 y1≥y2≥⋯yn,这样的标量积为 S1=x1×y1+x2×y2+⋯+xn×yn。
假设存在另一种配对方式,存在两个位置 i 和 j,xi 和 yj 配对,xj 和 yi 配对,且这种配对的标量积 S2<S1,则需要满足 xi×yi+xj×yj>xi×yj+xj×yi。
考虑两种配对方式带来的差异:
- xi 和 yi 配对,xj 和 yj 配对,和为 xi×yi+xj×yj。
- xi 和 yj 配对,xj 和 yi 配对,和为 xi×yj+xj×yi。
我们计算差值,以此比较大小:
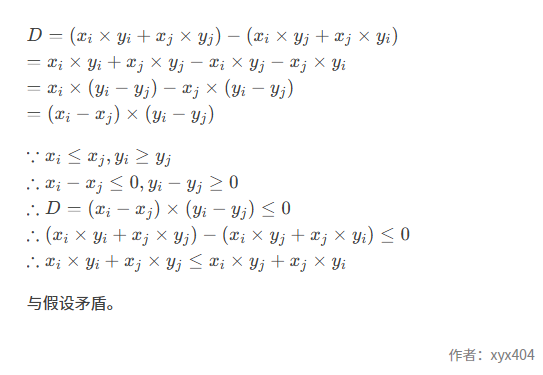
因此,不存在比 v1 升序,v2 降序的配对方式更小的标量积。
故代码正确。


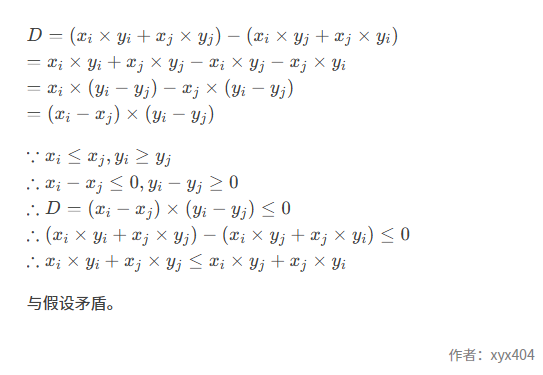







![题解:P14041 [PAIO 2025] Towers](https://fastly.jsdelivr.net/npm/xyx404blogphoto@1.2.65/P14041.jpg)

